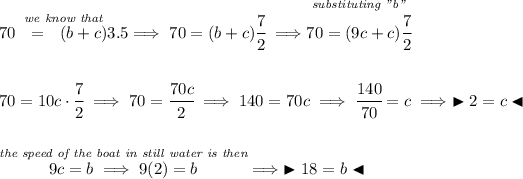Question

a motorboat travels a distance of one pier to another pier in 4 hrs and the way back in 5 hrs. What is the speed of the boat in still water if it travels 70 km with the current in 3.5 hrs?

Answer 1

let's recall that d = rt, namely distance = rate * time.

d = distance from one pier to another

c = speed of the current

b = speed of the boat

now, let's notice something, on the way over the boat travelled "d" kilometers in 4 hrs, and back the same "d" kilometers in 5 hours.

when going with the current, the boat is not really going at "b" km/s, is really going faster, at "b + c" km/s, because the current is adding to it.

now, when going against the current, the boat is not really going "b" fast, is really going slower, at "b - c", because the current is subtracting from it.

from the above, we can conclude that the 4hrs trip was with the current, since it took less time, and the 5hrs trip was against the current, and we also know that the boat does 70 km with the current in 3.5 hrs, ok hmmm let's put all that in a table.

`\begin{array}{lcccl} &\stackrel{km}{distance}&\stackrel{km/h}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ \textit{on the way over}&d&b+c&4\\ \textit{on the way back}&d&b-c&5\\\cline{1-4} \textit{we also know}&70&b+c&3.5 \end{array}~\hfill \begin{cases} d=(b+c)4\\\\ d = (b-c)5 \end{cases} \\\\\\ \stackrel{\textit{substituting on the 2nd equation}}{(b+c)4~~ = ~~(b-c)5}\implies 4b+4c=5b-5c \\\\\\ 4c=b-5c\implies \boxed{9c=b} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{we know that}}{70~~ = ~~(b+c)3.5}\implies 70=(b+c)\cfrac{7}{2}\implies \stackrel{\textit{substituting`