Answer:
16.63min
Step-by-step explanation:
The question is about the period of the comet in its orbit.
To find the period you can use one of the Kepler's law:

T: period
G: Cavendish constant = 6.67*10^-11 Nm^2 kg^2
r: average distance = 1UA = 1.5*10^11m
M: mass of the sun = 1.99*10^30 kg
By replacing you obtain:
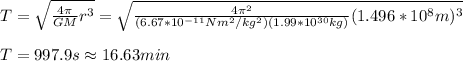
the comet takes around 16.63min