Answer:
The expected repair cost is $3.73.
Explanation:
The random variable X is defined as the number of defectives among the 4 items sold.
The probability of a large lot of items containing defectives is, p = 0.09.
An item is defective irrespective of the others.
The random variable X follows a Binomial distribution with parameters n = 9 and p = 0.09.
The repair cost of the item is given by:
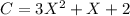
Compute the expected cost of repair as follows:
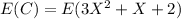

Compute the expected value of X as follows:
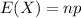

The expected value of X is 0.36.
Compute the variance of X as follows:
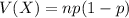
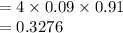
The variance of X is 0.3276.
The variance can also be computed using the formula:
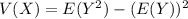
Then the formula of
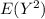 is:
is:
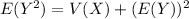
Compute the value of
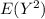 as follows:
as follows:
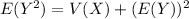
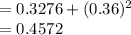
The expected repair cost is:

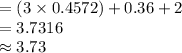
Thus, the expected repair cost is $3.73.