Answer:
the mass of steam at 100°C must be mixed is 150 g
Step-by-step explanation:
given information:
ice's mass,
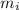 = 490 g = 0.49 kg
= 490 g = 0.49 kg
steam temperature, T = 100°C
liquid water temperature, T = 89.0°C
specific heat of water,
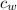 = 4186 J/kg.K = 4.186 kJ/kg.K
= 4186 J/kg.K = 4.186 kJ/kg.K
latent heat of fusion,
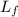 = 333 kJ/kg
= 333 kJ/kg
latent heat of vaporization,
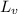 = 2256 kJ/kg
= 2256 kJ/kg
first, we calculate the heat of melted ice to water
Q₁ =

where
Q = heat
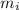 = mass of the ice
= mass of the ice
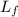 = latent heat of fusion
= latent heat of fusion
thus,
Q₁ =

= 0.49 x 333
= 163.17 kJ
then, the heat needed to increase the temperature of water to 89.0°C
Q₂ =
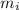
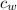 (89 - 0), the temperature of ice is 0°C
(89 - 0), the temperature of ice is 0°C
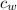 = specific heat of water
= specific heat of water
so,
Q₂ =
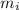
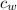 (89 - 0)
(89 - 0)
= 0.49 x 4.186 x 89
= 182.55 kJ
so, the heat absorbed by the ice is
Q = Q₁ + Q₂
= 163.17 + 182.55
= 345.72 kJ
the temperature of the steam is 100°C, so the mass of the steam is
Q =
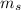
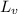 +
+
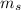
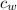 (100 - 89)
(100 - 89)
Q =
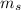 (
(
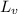 +
+
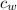 (11))
(11))
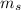 = Q/ [
= Q/ [
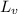 +
+
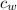 (11)]
(11)]
= 345.72/ [2256 + (4.186 x 11)]
= 0.15 kg
= 150 g