Answer:
1. Sample Mean = 2.50
2. Sample Variance = 1.35
3. Standard Deviation = 1.16
Explanation:
Note: As this question is not complete, similar can be found on internet where following are asked to calculate and here I will calculate these as well.
1. Sample Mean.
2. Sample Variance.
3. Sample Standard Deviation.
So, for sample mean to calculate from the given data points. We need to apply to following formula to calculate sample mean.
Sample Mean = (X1 + X2 + .... + XN) divided by Total number of data points.
Sample Mean = (0.17 + 1.94 + 2.62 + 2.35 + 3.05 + 3.15 + 2.53 + 4.81 + 1.92) divided by (9).
Sample Mean = 2.50
Likewise, from the answer of sample mean we can calculate sample variance by following steps.
Solution:
1. Subtract the obtained mean from each of the data point given.
(0.17 - 2.50) = -2.33
(1.94 - 2.50) = -0.56
(2.62 - 2.50) = 0.12
(2.35 - 2.50) = -0.15
(3.05 - 2.50) = 0.55
(3.15 - 2.50) = 0.65
(2.53 - 2.50) = 0.03
(4.81 - 2.50) = 2.31
(1.92 - 2.50) = -0.58
2. Square each of the differences obtained in step 1.
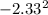 = 5.43
= 5.43
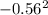 = 0.31
= 0.31
 = 0.01
= 0.01
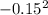 = 0.02
= 0.02
 = 0.30
= 0.30
 = 0.42
= 0.42
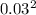 = 0.01
= 0.01
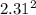 = 5.34
= 5.34
 = 0.34
= 0.34
3. Sum all of these squares.
(5.43 + 0.31 + 0.01 + 0.02 + 0.30 + 0.42 + 0.01 + 5.34 + 0.34) = 12.18
4. Divide 12.18 by (n-1), where n = 9.
Sample Variance = 12.18/9 = 1.35
Now, by using sample variance, we can calculate standard deviation with easy simple steps.
So, in order to find standard deviation, we just need to take the square root of sample variance that we have already calculated above.
Standard Deviation =
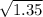 = 1.16
= 1.16
Good Luck!