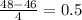Question

A sample is selected from a population with μ = 46, and a treatment is administered to the sample. After treatment, the sample mean is μ = 48 with a sample variance of σ² = 16. Based on this information, what is the value of Cohen’s d?

Answer 1

0.5

Explanation:

Solution:-

- The sample mean before treatment, μ1 = 46

- The sample mean after treatment, μ2 = 48

- The sample standard deviation σ = √16 = 4

- For the independent samples T-test, Cohen's d is determined by calculating the mean difference between your two groups, and then dividing the result by the pooled standard deviation.

Cohen's d =
`(u2 - u1)/(sd_p_o_o_l_e_d)`

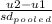
- Where, the pooled standard deviation (sd_pooled) is calculated using the formula:

`sd_p_o_o_l_e_d =\sqrt{(SD_1^2 +SD_2^2)/(2) }`

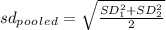
- Assuming that population standard deviation and sample standard deviation are same:

SD_1 = SD_2 = σ = 4

- Then,

`sd_p_o_o_l_e_d =\sqrt{(4^2 +4^2)/(2) } = 4`

- The cohen's d can now be evaliated:

Cohen's d =
`(48 - 46)/(4) = 0.5`