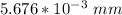Question

A surgical microscope weighing 200 lb is hung from a ceiling by four springs with stiffness 25 lb/ft. The ceiling has a vibration amplitude of 0.05mm at 2 Hz (a typical resonant frequency of a building). a) If there is no damping, how much transmitted vibration (amplitude of displacement) does the microscope experience

Answer 1

If there is no damping, the amount of transmitted vibration that the microscope experienced is =
`5.676*10^(-3) \ mm`

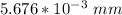
Step-by-step explanation:

The motion of the ceiling is y = Y sinωt

y = 0.05 sin (2 π × 2) t

y = 0.05 sin 4 π t

K = 25 lb/ft × 4 sorings

K = 100 lb/ft

Amplitude of the microscope
`(X)/(Y)= [(1+2 \epsilon (\omega/ W_n)^2)/((1-((\omega)/(W_n))^2)^2+(2 \epsilon (\omega)/(W_n))^2)]`

where;

`\epsilon = 0`

`W_n = \sqrt { (k)/(m)}`

=
`\sqrt { (100*32.2)/(200)}`

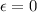
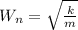
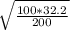
= 4.0124

replacing them into the above equation and making X the subject of the formula:

`X =`
`Y * \frac{1}{\sqrt{(1-((\omega)/(W_n))^2)^2})}}`

`X =`
`0.05 * \frac{1}{\sqrt{(1-((4 \pi)/(4.0124))^2)^2})}}`

`X =`
`5.676*10^(-3) \ mm`

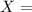
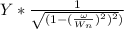
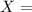
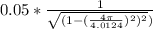
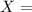
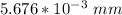
Therefore; If there is no damping, the amount of transmitted vibration that the microscope experienced is =
`5.676*10^(-3) \ mm`