Question

A manufacturer of hard safety hats for construction workers is concerned about the mean and the variation of the forces its helmets transmit to wearers when subjected to a standard external force. The manufacturer desires the mean force transmitted by helmets to be 800 pounds (or less), well under the legal 1000-pound limit, and desires σ to be less than 40. Tests were run on a random sample of n = 40 helmets, and the sample mean and variance were found to be equal to 825 pounds and 2350 pounds2 , respectively.Construct a 95% confidence interval for the population variance.

Answer 1

Explanation:

Hello!

You need to construct a 95% CI for the population variance of the forces the safety helmets transmit to wearers.

The variable of interest is X: Force a helmet transmits its wearer when an external force is applied (pounds)

Assuming this variable has a normal distribution, the manufacturer expects it to have a mean of μ= 800 pounds and a standard deviation of σ= 40 pounds

A test sample of n=40 was taken and the resulting mean and variance are:

X[bar]= 825 pounds

S²= 2350 pounds²

To estimate the population variance per confidence interval you have to use the following statistic:

`X^2= ((n-1)S^2)/(Sigma^2) ~~X^2_(n-1)`

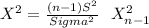
And the CI is calculated as:

[
`((n-1)S^2)/(X^2_(n-1;1-\alpha /2))`;
`((n-1)S^2)/(X^2_(n-1;\alpha /2))`]

`X^2_(n-1;1-\alpha /2)= X^2_(39;0.975)= 58.1`

`X^2_(n-1;\alpha /2)= X^2_(39;0.025)= 23.7`

[
`(39*2350)/(58.1)`;
`(39*2350)/(23.7)`]

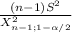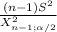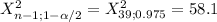
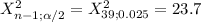
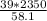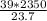[1577.45; 3867.09] pounds²

Using a confidence level of 95% you'd expect that the interval [1577.45; 3867.09] pounds² contains the value of the population variance of the force the safety helmets transmit to their wearers when an external force is applied.

I hope this helps!