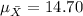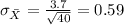Answer:
Let X the random variable that represent the delivery times of a population, and for this case we know the distribution for X is given by:

Where
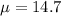 and
and
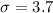
Since the distribution of X is normal then we know that the distribution for the sample mean
 is given by:
is given by:

And we have;
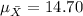
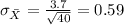
Explanation:
Assuming this question: The delivery times for all food orders at a fast-food restaurant during the lunch hour are normally distributed with a mean of 14.7 minutes and a standard deviation of 3.7 minutes. Let R be the mean delivery time for a random sample of 40 orders at this restaurant. Calculate the mean and standard deviation of
 Round your answers to two decimal places.
Round your answers to two decimal places.
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Solution to the problem
Let X the random variable that represent the delivery times of a population, and for this case we know the distribution for X is given by:

Where
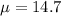 and
and
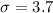
Since the distribution of X is normal then we know that the distribution for the sample mean
 is given by:
is given by:

And we have;