Answer:
1. 8.378
2. 3.534
3. 12.566
4. 0.262 rad or
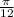
5. 1.222 rad or
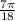
6. 5.236 rad or

7. 240°
8. 165°
9. 22.5°
10. 30° =
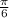 radians
radians
45° =
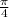 radians
radians
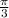 radians = 60°
radians = 60°
 radians = 90°
radians = 90°
120° =
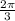 radians
radians
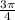 radians = 45°
radians = 45°
 radians = 180°
radians = 180°
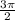 radians = 270°
radians = 270°
360° =
 radians
radians
11. 9.424 inches
Explanation:
Problems 1-3:
S=r*Ф
S= arc length, r= radius, Ф= angle in radians
You need to convert the angle from degrees to radians before you can use it in the equation. You do this by multiplying it by pi and dividing by 180. Then you can plug this and the radius into the equation to solve for the arc length.
1) 120° x
 = 2.094 rad
= 2.094 rad
S= 4 x 2.094 = 8.378
2) 135° x
 = 2.356 rad
= 2.356 rad
S= 1.5 x 2.356 = 3.534
3) 240° x
 = 4.189 rad
= 4.189 rad
S= 3 x 4.189 = 12.566
Problems 4-6:
4) 15° x
 = 0.262 rad or
= 0.262 rad or
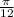
5) 70° x
 = 1.222 rad or
= 1.222 rad or
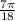
6) 300° x
 = 5.236 rad or
= 5.236 rad or

Problems 7-9:
7)
 240°
240°
8)
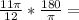 165°
165°
9)
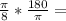 22.5°
22.5°
Problem 10:
30° =
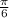 radians
radians
45° =
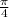 radians
radians
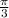 radians = 60°
radians = 60°
 radians = 90°
radians = 90°
120° =
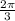 radians
radians
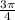 radians = 45°
radians = 45°
 radians = 180°
radians = 180°
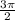 radians = 270°
radians = 270°
360° =
 radians
radians
Problem 11:
S= r * Ф
S= 4 *
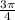
S= 3
 = 9.424 inches
= 9.424 inches