Question

After creating a Beer's Law plot using standard solutions of Q, you determined the slope of Beer's Law to be 0.543 M-1. Your unknown solution of Q tested in Part B of the experiment had an absorbance of 0.144. Determine the concentration (in molarity) of the unknown solution Q from Part B. Do not use scientific notation or units in your response. If Carmen adds zeros after the decimal place, your answer will still be graded correctly.

Answer 1

Answer : The concentration (in molarity) of the unknown solution Q is, 0.265

Explanation :

Using Beer-Lambert's law :

`A=\epsilon * C* l`

where,

A = absorbance of solution

C = concentration of solution

l = path length

`\epsilon` = molar absorptivity coefficient

From the Beer's Law plot between absorbance and concentration we concldue that the slope is equal to
`\epsilon * l` and path length is 1 cm.

As we are given that:

Slope = 0.543 M⁻¹

and,

Slope =
`\epsilon * l`

`\epsilon * l=0.543M^(-1)`

`\epsilon * 1cm=0.543M^(-1)`

`\epsilon=0.543M^(-1)cm^(-1)`

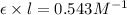
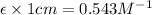
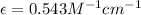
Now we have to determine the concentration (in molarity) of the unknown solution Q.

Using Beer-Lambert's law :

`A=\epsilon * C* l`

`0.144=0.543M^(-1)cm^(-1)* C* 1cm`

`C=0.265M`

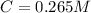
Therefore, the concentration (in molarity) of the unknown solution Q is, 0.265