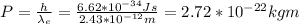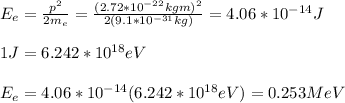Question

X rays of wavelength 0.0169 nm are directed in the positive direction of an x axis onto a target containing loosely bound electrons. For Compton scattering from one of those electrons, at an angle of 132°, what are (a) the Compton shift, (b) the corresponding change in photon energy, (c) the kinetic energy of the recoiling electron, and (d) the angle between the positive direction of the x axis and the electron's direction of motion? The electron Compton wavelength is 2.43 × 10-12 m.

Answer 1

a) 4.04*10^-12m

b) 0.0209nm

c) 0.253MeV

Step-by-step explanation:

The formula for Compton's scattering is given by:

`\Delta \lambda=\lambda_f-\lambda_i=(h)/(m_oc)(1-cos\theta)`

where h is the Planck's constant, m is the mass of the electron and c is the speed of light.

a) by replacing in the formula you obtain the Compton shift:

`\Delta \lambda=(6.62*10^(-34)Js)/((9.1*10^(-31)kg)(3*10^8m/s))(1-cos132\°)=4.04*10^(-12)m`

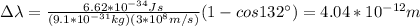
b) The change in photon energy is given by:

`\Delta E=E_f-E_i=h(c)/(\lambda_f)-h(c)/(\lambda_i)=hc((1)/(\lambda_f)-(1)/(\lambda_i))\\\\\lambda_f=4.04*10^(-12)m +\lambda_i=4.04*10^(-12)m+(0.0169*10^(-9)m)=2.09*10^(-11)m=0.0209nm`

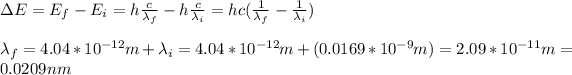
c) The electron Compton wavelength is 2.43 × 10-12 m. Hence you can use the Broglie's relation to compute the momentum of the electron and then the kinetic energy.

`P=(h)/(\lambda_e)=(6.62*10^(-34)Js)/(2.43*10^(-12)m)=2.72*10^(-22)kgm\\`

`E_e=(p^2)/(2m_e)=((2.72*10^(-22)kgm)^2)/(2(9.1*10^(-31)kg))=4.06*10^(-14)J\\\\1J=6.242*10^(18)eV\\\\E_e=4.06*10^(-14)(6.242*10^(18)eV)=0.253MeV`