Question

Three concentric circles have radii 5, 10, 15. Chords of the 2 larger circles are tangent to the 2 smaller circles, respectively, and the points of tangency lie on the same radius of the largest circle. Find the area of the trapezoidal region determined by the endpoints of the chords.

Answer 1

Area of the trapezoidal region = 99 square units

Explanation:

Let the common center of the three circles be O and OA to be the radius of the larger circle, intersecting the smallest circle and middle circle at B and C, respectively.

Where DE be the chord of the middle circle and FG be the chord of the largest circle as shown on the diagram.

We have to find the area of the trapezoidal region EDFG.

Formula to be used:

Area of a trapezium : 1/2 (sum of parallel sides) (height)

Or

Area of a trapezium : 1/2 (DE + FG) (BC)

We know that:

The tangent to a circle is perpendicular to the radius at the point of tang-ency.

So,

We have to find DH and FG.

In ΔOBE :

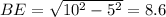`BE=√(10^2-5^2) = 8.6` ...Using Pythagoras formula.

`DE = 2 (BE) = 2(8.6) = 17.2`

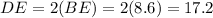
In ΔOCF :

`CF=√(15^2-10^2) = 11.2`

`FG = 2 (CF) =2(11.2) =22.4`

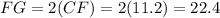
Plugging the values in the area equation.

⇒
`Area = ((DE + FG)* (BC))/(2)`

⇒
`Area = ((17.2+22.4)* (5))/(2)`

⇒
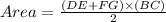
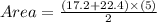
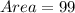`Area = 99` square unit

The area of the trapezoidal region determined by the endpoints of the chords will be 99 square unit.