Question

Stochastic n-by-n matrices Recall that an n × n matrix A is said to be stochastic if the following conditions are satisfied (a) Entries of A are non negative, that is ai,j ≥ 0 for all 1 ≤ i ≤ n and all 1 ≤ j ≤ n. (b) Each column of A sums to 1, that is Pn i=1 ai,j = 1, for all 1 ≤ j ≤ n. Let S and M be arbitrary stochastic n-by-n matrices. (a) Show that λ = 1 is an eigenvalue of S. 2 points (b) Show that S 2 is also a stochastic matrix. 2 points (c) Does MS have to be stochastic? Explain

Answer 1

a) Entries of A are non negative, that is ai,j ≥ 0 for all 1 ≤ i ≤ n and all 1 ≤ j ≤ n.

c) yes MS is stochastic

Explanation:

a) A stochastic matrix is a square matrix whose columns are probability vectors. A probability vector is a numerical vector whose entries are real numbers between 0 and 1 whose sum is 1.

B)

a) Now, suppose Sx=λx for some λ>1. Since the rows of S are nonnegative and sum to 1, each element of vector Sx is a convex combination of the components of x, which can be no greater than maximum of x the largest component of x. On the other hand, at least one element of λx is greater than maximum of x, which proves that λ>1 is impossible and Hence λ = 1.

b) Then
`S^(2)` =
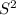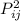`P^(2)_(ij)` is also stochastic; it is the two-step transition matrix for the chain {Xn, n = 0,1,…}. To every stochastic matrix S, there corresponds a Markov chain {Xn} for which S is the unit-step transition matrix.

However, not every stochastic matrix is the two-step transition matrix of a Markov chain.

c) Let A and B be two row-stochastic matrices and suppose we know the product of column stochastic matrices is column-stochastic. Observe that,

MS =
`((MS)^(T))^(T) = (S^(T)M^(T))^(T)`

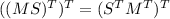
by properties of transpose of a matrix. Let us consider
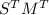`S^(T) M^(T)`. It is easy to see that the transpose of a row-stochastic matrix is column-stochastic by definition (and vice versa). Thus,
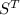`S^(T)`and
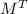`M^(T)` are column stochastic and by our assumption, it must then be the case that
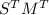`S^(T) M^(T)` is column-stochastic. Since
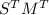`S^(T) M^(T)` is column-stochastic, then it's transpose
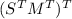`(S^(T) M^(T))^(T)`=MS is row stochastic.