Question

A wheel, starting from rest, rotates with a constant angular acceleration of 2.80 rad/s2. During a certain 5.00 s interval, it turns through 65.0 rad. (a) How long had the wheel been turning before the start of the 5.00 s interval? (b) What was the angular velocity of the wheel at the start of the 5.00 s interval?

Answer 1

a. The wheel was turning 2.14 s before the start of the 5.00 s interval.

b. The angular velocity of the wheel at the start of the 5.00 s interval was 6.00 rad/s.

Step-by-step explanation:

At the start of the 5.00s interval, the wheel might have an initial angular velocity
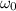`\omega_0`. We can obtain it from the kinematic equation:

`\theta=\omega_0t+(1)/(2)\alpha t^(2)\\\\\implies \omega_0=(\theta)/(t)-(1)/(2)\alpha t`

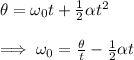
Plugging in the known values for the time interval, the angular displacement and the angular acceleration, we get:

`\omega_0=(65.0rad)/(5.00s)-(1)/(2)(2.80rad/s^(2))(5.00s)\\\\\omega_0=6.00rad/s`

It means that the angular velocity of the wheel at the start of the 5.00 s interval was 6.00 rad/s (b).

The time it took for the wheel to reach that angular velocity can be obtained from another kinematic equation:

`\omega = \omega_0+\alpha t\\\\\implies t=(\omega-\omega_0)/(\alpha)`

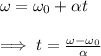
It is important to take in account that in this case, the initial angular velocity is zero as the wheel started from rest, and the final angular velocity is the one we got in the previous question:

`t=(6.00rad/s-0)/(2.80rad/s^(2))\\\\t=2.14s`

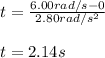
Finally, the wheel was turning 2.14 s before the start of the 5.00 s interval (a).

Answer 2

a) time t1 = 2.14s

b) initial angular speed w1 = 6 rad/s

Step-by-step explanation:

Given that;

Initial Angular velocity = w1

Angular distance = s = 65 rad

time = t = 5 s

Angular acceleration a = 2.80 rad/s^2

Using the equation of motion;

s = w1t + (at^2)/2

w1 = (s-0.5(at^2))/t

Substituting the values;

w1 = (65 - (0.5×2.8×5^2))/5

w1 = 6rad/s

Time to reach w1 from rest;

w1 = at1

t1 = w1/a = 6/2.8 = 2.14s

a) time t1 = 2.14s

b) initial angular speed w1 = 6 rad/s