Question

g Suppose that the number of bacteria in a certain population increases according to a continuous exponential growth model. A sample of 3000 bacteria selected from this population reached the size of 3145 bacteria in one and a half hours. Find the hourly growth rate parameter. Note: This is a continuous exponential growth model. Write your answer as a percentage. Do not round any intermediate computations, and round your percentage to the nearest hundredth.

Answer 1

The hourly growth rate is of 3.15%

Explanation:

The population of bacteria after t hours can be modeled by the following formula:

`P(t) = P(0)e^(rt)`

In which P(0) is the initial population and r is the hourly growth parameter, as a decimal.

A sample of 3000 bacteria selected from this population reached the size of 3145 bacteria in one and a half hours. Find the hourly growth rate parameter.

This means that
`P(0) = 3000, P(1.5) = 3145`

We use this to find r.

`P(t) = P(0)e^(rt)`

`3145 = 3000e^(1.5r)`

`e^(1.5r) = (3145)/(3000)`

`\ln{e^(1.5r)} = \ln{(3145)/(3000)}`

`1.5r = \ln{(3145)/(3000)}`

`r = \frac{\ln{(3145)/(3000)}}{1.5}`

`r = 0.0315`

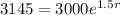
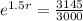
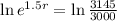
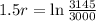
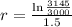
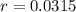
The hourly growth rate is of 3.15%