Answer:
263.8 m/s2
Step-by-step explanation:
Assume this is a solid disk, we can find its moments of inertia:
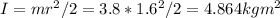
The torque T generated by force F = 18.4N is:
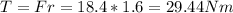
So the angular acceleration of the disk according to Newton's 2nd law is:
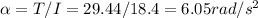
If the disk starts from rest, then after 3s its angular speed is
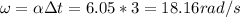
And so its radial acceleration at this time and half way from the center to the edge is:
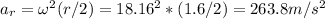
Note that this value is the same anywhere