Question

The voltage V in a simple electrical circuit is slowly decreasing as the battery wears out. The resistance R is slowly increasing as the resistor heats up. Use Ohm's Law, V = IR, to find how the current I is changing at the moment when R = 337Ω, I = 0.01A, dV/dt = -0.07V/s, and dR/dt = 0.06Ω/s. (Round your answer to six decimal places.)

Answer 1

The current is decreasing at a rate 0.000209 ampere per second.

Explanation:

We are given the following in the question:

`R = 337\Omega\\I = 0.01 A\\\\(dV)/(dt) = -0.07\text{ V/s}\\\\(dR)/(dt) = 0.06\text{ ohm/s}`

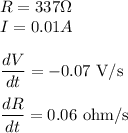
According to the Ohm's Law:

V = IR

Differentiating we get,

`(dV)/(dt) = I(dR)/(dt) + R(dI)/(dt)`

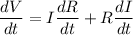
Putting values, we get,

`-0.07 = (0.01)(0.06)+ (337)(dI)/(dt)\\\\(337)(dI)/(dt) = -0.07-(0.01)(0.06) =-0.0706\\\\(dI)/(dt) = (-0.0706)/(337) = -0.000209\text{ A/s}`

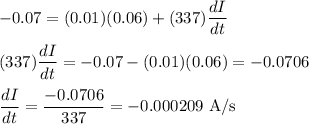
Thus, the current is decreasing at a rate 0.000209 ampere per second.