1 Answer

Konstantin Salavatov · Answer 1 · 2021-12-19T08:17:59+0000

Answer:

Option D) 0.65

Explanation:

We are given the following in the question:

Percentage of executives who read Time magazine = 35%

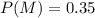
P(M) = 0.35

Percentage of executives who read U.S. News & World Report = 40%

P(N) = 0.4

Percentage of executives who read both Time magazine and U.S. News & World Report = 10%

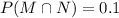
$P(M\cap N) = 0.1$

We have to find the probability that a particular top executive reads either Time or U.S. News & World Report regularly.

Thus, we have to evaluate,

$P(M\cup N) = P(M) + P(N) -P(M\cap N)$

Putting values, we get,

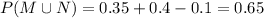
$P(M\cup N) = 0.35 + 0.4 - 0.1=0.65$

0.65 is the probability that a particular top executive reads either Time or U.S. News & World Report regularly.

Thus, the correct answer is

Option D) 0.65

Please log in or register to add a comment.