Answer:
The confidence interval for the proportion of students supporting the fee increase
( 0.77024, 0.81776)
Step-by-step explanation:
Step-by-step explanation:
Given data a survey of an urban university (population of 25,450) showed that 883 of 1,112 students sampled supported a fee increase to fund improvements to the student recreation center.
Given sample size 'n' = 1112
Sample proportion 'p' =
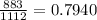
q = 1 - p = 1- 0.7940 = 0.206
The 95% level of confidence intervals
The confidence interval for the proportion of students supporting the fee increase
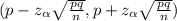
The Z-score at 95% level of significance =1.96
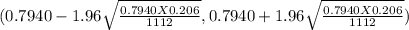
(0.7940-0.02376 , 0.7940+0.02376)
( 0.77024, 0.81776)
Conclusion:-
The confidence interval for the proportion of students supporting the fee increase
( 0.77024, 0.81776)