Answer:
The process does not meets the specifications.
Explanation:
It is provided that the Crunchy Potato Chip Company packages potato chips in a process designed for 10.0 ounces of chips.
The value of upper specification limit is, USL = 10.5 ounces.
The value of lower specification limit is, LSL = 9.5 ounces.
The mean weight of the chips bags is,
 .
.
And the standard deviation weight of the chips bags is,
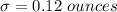 .
.
Compute the value of process capability as follows:
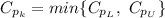
Compute the value of
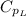 as follows:
as follows:
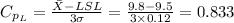
Compute the value of
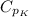 as follows:
as follows:
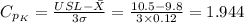
The value of process capability is:
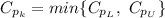
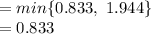
The value of process capability lies in the interval 0 to 1. So the process is not capable of meeting design specifications.
Thus, the process does not meets the specifications.