Answer:
1) 1.1 x
 m
m
2)2.51 x
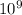 Pa
Pa
Step-by-step explanation:
Given:
Speed of sound in prostate 'V'= 1540m/s
frequency 'f' = 1.40 MHz = 1.40 x
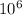 Hz
Hz
density of prostate'ρ' = 1060 kg/m3
1) As we know that the relationship of the speed of sound, its frequency, and wavelength is the same as for all waves
V= fλ
λ= V/f => 1540/1.40 x
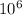
λ= 1.1 x
 m
m
Thus, the wavelength of the sonogram ultrasound is 1.1 x
 m
m
2)The speed of sound in a solid the depends on the Young's modulus of the medium and the density
V=√Y/ρ.
V² = Y/ρ
Y= V² x ρ=> 1540² x 1060
Y= 2.51 x
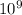 Pa
Pa
Thus, Young's modulus for the prostate gland is 2.51 x
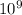 Pa
Pa