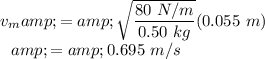Answer:
The greatest extension of the spring is
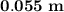 and the maximum speed of the block is
and the maximum speed of the block is
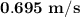 .
.
Step-by-step explanation:
Given:
The mass of the block is,
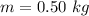
The spring constant of the spring is,
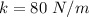
The mechanical energy of the block is,
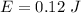
When a particle is oscillating in a simple harmonic way, its total energy is given by

where
 is the angular velocity of the mass and
is the angular velocity of the mass and
 is the amplitude of its motion.
is the amplitude of its motion.
The relation between angular velocity and spring constant is given by

Substituting equation (2) in equation (1), we have
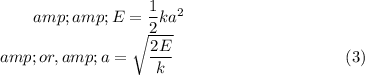
Substituting
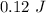 for
for
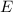 and
and
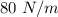 for
for
 in equation (3), we can write
in equation (3), we can write
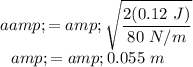
The relation between the maximum velocity and the amplitude is given by

Substituting
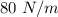 for
for
 ,
,
 for
for
 and
and
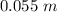 for
for
 in equation (4), we have
in equation (4), we have