Answer:

Explanation:
Hello!
Given the probability information about analyst's report (Good, Medium, and Bad) and the earnings announcement (Forecast), you have to calculate the probability that the analyst issued a good report, given that the earnings announcement was "bellow the forecast".
Symbolically: P(Good Report/Below Forecast)
This is a conditional probability, a little reminder:
If you have the events A and B, that are not independent, the probability of A given that B has already happened can be calculated as:
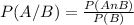
Where P(A∩B) is the intersection between the two events and P(B) represents the marginal probability of ocurrence of B.
*-*
Using that formula:

As you can see you have to calculate the value of the probability for the intersection between "Good report" and "Below Forecast" and the probability for P(Below Forecast)
Using the given probability values you can clear the value of the intersection:
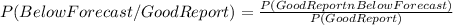
P(Good Report ∩ Below Forecast)= P(BelowForecast/GoodReport)*P(Good Report)= 0.1*0.2= 0.02
Now the probability of an earnings announcement being "Below Forecast" is marginal, that is if you were to arrange all possible outcomes in a contingency table this probability will be in the marginal sides of the table:
Below Forecast
Good Report P(GoodR∩BelowF)
Medium Report P(MediumR∩BelowF)
Bad Report P(BadR∩BelowF)
Total P(Below Forecast)
Then P(BelowF)=P(GoodR∩BelowF)+P(MediumR∩BelowF)+P(BadR∩BelowF)
You can clear the two missing probabilities from the remaining information:
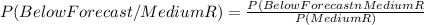
P(BelowF∩MediumR)= P(BelowF/MediumR)*P(MediumR)= 0.4*0.5= 0.2
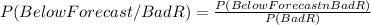
P(BelowF∩BadR)= P(BelowF/BadR)*P(BadR)= 0.9*0.3= 0.27
Now you can calculate the probability of the earning announcement being below forecast:
P(BelowF)=P(GoodR∩BelowF)+P(MediumR∩BelowF)+P(BadR∩BelowF)
P(BelowF)= 0.02+0.2+0.27= 0.49
And finally the asked probability is:

I hope this helps!