Question

A research team conducted a critical study, and using the data they gathered in their random experiment, a 95% confidence interval for the population mean was constructed. The team was not happy with the result because they felt the margin of error was much too large. All other things being equal, if they were to repeat the study, what could they do to reduce the margin of error

Answer 1

Increasing sample size (n), decreasing the standard deviation or decreasing the confidence level will reduce the margin of error.

Explanation:

The (1 - α)% confidence interval for population mean μ is:

`CI=\bar x\pm CV* (SD)/(√(n))`

The margin of error for this interval is:

`MOE=CV* (SD)/(√(n))`

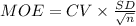
So, the factors affecting the margin of error are:

• Confidence level
• Standard deviation
• Sample size

It is provided that the team was not happy with the result of the 95% confidence interval constructed, because they felt the margin of error was much too large.

To reduce the margin of error:

• Increase the sample size.

Since the sample is inversely proportional to the margin of error, increasing the value of n will decrease the MOE.

• Decrease the standard deviation.

The standard deviation is directly proportional to the margin of error. On decreasing the standard deviation value the MOE of the interval will also decrease.

• Decrease the confidence level.

The critical value of the distribution is based on the confidence level. Higher the confidence level, higher will be critical value.

So, on deceasing the confidence level the critical value will decrease, hence decreasing the margin of error.