Answer:
d. As the sample size decreases, the margin of error increases.
Explanation:
Hello!
The population proportion of students that are allowed to use cell phones in classrooms was estimated using a random sample of n=250 college students obtaining a margin of error of d= 0.061
The formula of the CI interval for the population proportion is:
p' ±
 *
*
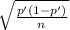
Where
p'= sample proportion ⇒ point estimation of the population proportion
d=
 *
*
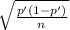 ⇒ margin of error of the interval
⇒ margin of error of the interval
As you can see in the formula, the sample size (n) and the margin of error (d) have an indirect relationship, this means, that when the sample size increases, the margin of error decreases and vice versa.
So if you decrease the sample size from 250 to 125 students, you will expect the margin of error to increase:
Using p'= 0.40 and Z= 1.96
d''=
 *
*
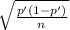
d''= 1.96 *
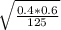
d''= 0.086
As expected, the margin of error of the CI is greater when the sample size is reduced. This means that the estimation of the population proportion is less accurate when a smaller sample is taken.
I hope this helps!