Question

Maria is planning to attend UCLA. She is curious what the average age of UCLA students is. Since most students that attend UCLA are in their 20’s yet there are also students up to 70 years old, the population is positively skewed. The college conducted a random sample of 65 students and found that the sample mean was 29.0 years old with a standard deviation of 5.2 years. Does this data meet the assumptions necessary to perform a hypothesis test? If so, use a 10% significance level to test the claim that the average age of students at UCLA is 30 years old.

Answer 1

Yes

We fail to reject the alternative hypothesis Hₐ < 30, that is the average age of students is less than 30

Explanation:

Yes because, there is an average age of a sample which can be tested against a null hypotheses

We put

Null hypothesis as H₀ = 30

The alternative hypothesis as Hₐ < 30

We have

`z=\frac{\bar{x}-\mu }{(\sigma )/(√(n))}`

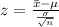
With

`\bar x` = 29

μ = 30

σ = 5.2

n = 65

α = 10%

We have

Here we have z = -1.55 and critical z = -1.28

Which gives a critical
`\bar x` of 29.83 with the probability P = 0.061 < 0.1 Hence we reject the null hypothesis as there is sufficient evidence to suggest that the average age is less than 30 years.