Answer:
To Prove:
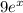 is equal to the sum of its Maclaurin series.
is equal to the sum of its Maclaurin series.
Explanation:
If
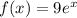 , then
, then
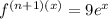 for all n. If d is any positive number and |x| ≤ d, then
for all n. If d is any positive number and |x| ≤ d, then

So Taylor's Inequality, with a = 0 and M =
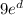 , says that
, says that
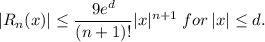
Notice that the same constant
 works for every value of n.
works for every value of n.
But, since
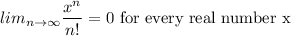 ,
,
We have
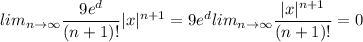
It follows from the Squeeze Theorem that
 and therefore
and therefore
 for all values of x.
for all values of x.
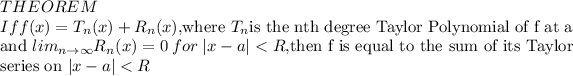
By this theorem above,
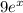 is equal to the sum of its Maclaurin series, that is,
is equal to the sum of its Maclaurin series, that is,
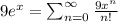 for all x.
for all x.