Question

Bottles of a popular cola drink are supposed to contain 300 ml of cola. There is some variation from bottle to bottle because the filling machinery is not perfectly precise. The distribution of the contents is normal with standard deviation of 3 ml. A student who suspects that the bottler is under-filling measures the contents of six bottles. The results are:299.4 297.7 301.0 298.9 300.2 297.0Is this convincing evidence that the mean contents of cola bottles is less than the advertised300 ml? Test at the 5% significance level.

Answer 1

No because there is sufficient statistical evidence to suggest that the mean contents of cola bottles is equal to 300 ml as advertised

Explanation:

Here we have the measured contents as

299.4

297.7

301.0

298.9

300.2

297.0

Total = 1794.2

∴ Mean = 299.03

Standard deviation = 1.5

We have

`z=\frac{\bar{x}-\mu }{(\sigma )/(√(n))}`

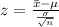
Where:

`\bar x` = Mean of sample = 299.03 ml

μ = Mean of population = 300 ml

σ = Standard deviation of population = 3 ml

n = Sample size = 6

α = 5% = 0.05

We set our null hypothesis as H₀ = 300 ml

Our alternative hypothesis is then Hₐ < 300 ml

Therefore, z = -0.792

The probability from z table is P = 0.2142

Since the P value, 0.2142 is > than the 5% significance level, 0.05 we accept the null hypothesis that the mean contents of cola bottles is 300 ml.