Question

We intend to estimate the average driving time of a group of commuters. From a previous study, we believe that the average time is 42 minutes with a standard deviation of 9 minutes. We want our 90 percent confidence interval to have a margin of error of no more than plus or minus 3 minutes. What is the smallest sample size that we should consider

Answer 1

The minimum sample size required is 25 so that margin of error is no more than 3 minutes.

Explanation:

We are given the following in the question:

Mean, μ = 42 minutes

Standard Deviation, σ = 9 minutes.

We want to build a 90% confidence interval such that margin of error is no more than 3 minutes.

Formula for margin of error:

`z_(critical)* (\sigma)/(√(n))`

`z_(critical)\text{ at}~\alpha_(0.10) = 1.64`

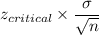
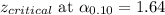
Putting values, we get.

`z_(critical)* (\sigma)/(√(n))\leq 3\\\\1.64* (9)/(√(n))\leq 3\\\\(1.64* 9)/(3)\leq √(n)\\\\4.92\leq √(n)\\\Rightarrow n\geq 24.2064\approx 25`

Thus, the minimum sample size required is 25 so that margin of error is no more than 3 minutes.