Answer:
~9.6 years it will be worth 3.23 mil.
Explanation:
This problem requires use of the growth formula.
PART 1:
Equation:
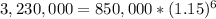
By solving this you get:
A valuation of $1,966,101.65078125 after 6 years
PART 2:
Equation:
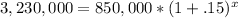
By solving this (which im too lazy to show the steps for) you get:
x = years
x = ~9.6 years / 9.55196417 years