Question

Desmond deposits $50 into a savings account every month at an annual interest rate of

4.7%, compounded monthly.
a. How much will his account contain after 10 years assuming he makes not withdrawals?
b. What is the rate of change in the value of Desmond’s account after 10 years?

Answer 1

Given:

Desmond deposits $ 50 monthly.

Yearly he deposits = $50×12 = $ 600

Rate of interest compounded monthly = 4.7%

To find the amount he will receive after 10 years and the rate of change the value of his account after 10 years.

Formula

`A = P(1+(r)/((n)(100)) )^(nt)`

where,

A be the final amount

P be the principal

r be the rate of interest

t be the time and

n be the number of times the interest is compounded.

Now,

Taking,

P = 600, r = 4.7, n = 12, t = 10 we get,

`A = 600(1+(4.7)/((12)(100))) ^((12)(10))`

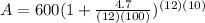
or,
`A = 600(1.0039)^(120)`

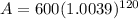
or,
`A = 959.1`

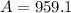
Now,

At starting he has $ 600

At the end of 10 years he will be having $ 959.1

So,

The amount of change in his account = $ (959.1-600) = $ 359.1

Therefore the rate of change =
`((359.1)/(600) )(100) %`

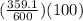
= 59.85%

Hence,

a) His account will contain $ 959.1 after 10 years.

b) The rate of change in his account is 59.85% after 10 years.