Answer:
There will be one person on 1 square yard of land after 1,892,147.588 years.
Explanation:
Continuous exponential growth formula:
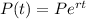
P(t)= Population after t years.
P= Initial population
r=rate of growth.
t= time in year
Given that,
Growth rate of country A (r)= 4.9% per year=0.049 per year.
Initial population (P)= 151,000.
Land area of country area= 14,000,000,000 square yards.
There will be one person on one square yard of land.
So, there will be 14,000,000,000 person for 14,000,000,000 square yard of land in country A.
P(t)=14,000,000,000 person
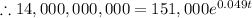
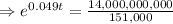
Taking ln both sides
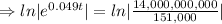
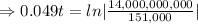
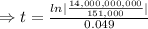
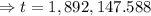 years
years
There will be one person for every square yard of land after 1,892,147.588 years.