Question

You are making an open box from a rectangular sheet of cardboard by cutting squares of equal length from each corner and folding up the sides. The dimensions of the sheet of cardboard are 15 inches by 12 inches. Write a polynomial that represents the total volume of the open box.

Answer 1

`V(x) = 4x^3 - 54x^2 + 180x`

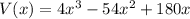
Explanation:

We are given the following in the question:

A rectangular piece of cardboard of side 15 inches by 12 inches is cut in such that a square is cut from each corner.

Let x be the side of this square cut. When it was folded to make the box.

The height of box =

`x\text{ inches}`

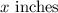
The length becomes

`(15-2x)\text{ inches}`

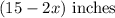
The width becomes

`(12-2x)\text{ inches}`

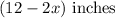
Volume of box =

`V =l* w* h`

Putting values, we get

`V(x) = (15-2x)(12-2x)x\\V(x) = (180-30x-24x+4x^2)(x)\\V(x) = (4x^2 - 54x + 180)(x)\\V(x) = 4x^3 - 54x^2 + 180x`

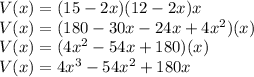
is the required polynomial for volume of box formed.