Question

Game consoles: A poll surveyed 341 video gamers, and 89 of them said that they prefer playing games on a console, rather than a computer or hand-held device. An executive at a game console manufacturing company claims that less than 28% of gamers prefer consoles. Does the poll provide convincing evidence that the claim is true? Use the =α0.05 level of significance and the P-value method with the TI-84 Plus calculator.

Answer 1

Explanation:

Hello!

The objective is to test if the population proportion of gamers that prefer consoles is less than 28% as the manufacturer claims.

Of 341 surveyed players, 89 said that they prefer using a console.

The sample resulting sample proportion is p'= 89/341= 0.26

If the company claims is true then p<0.28, this will be the alternative hypothesis of the test.

H₀: p ≥ 0.28

H₁: p < 0.28

α: 0.05

To study the population proportion you have to use the approximation of the standard normal
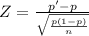`Z= \frac{p'-p}{\sqrt{(p(1-p))/(n) } }`≈N(0;1)

`Z_(H_0)= \frac{0.26-0.28}{\sqrt{(0.28*0.72)/(341) } }= -0.82`

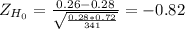
This test is one-tailed left, i.e. that you'll reject the null hypothesis to small values of Z, and so is the p-value, you can obtain it looking under the standard normal distribution for the probability of obtaining at most -0.82:

P(Z≤-0.82)= 0.206

Using the p-value approach:

If p-value ≤ α, reject the null hypothesis

If p-value > α, don't reject the null hypothesis

The decision is to not reject the null hypothesis.

Then at a level of 5%, you can conclude that the population proportion of gamers that prefer playing on consoles is at least 28%.

I hope this helps!