Question

An investment services company experienced dramatic growth in the last two decades. The following models for the company's revenue R and expenses or costs C (both in millions of dollars) are functions of the years past 1990. R(t) = 21.4e0.131t and C(t) = 18.6e0.131t (a) Use the models to predict the company's profit in 2020. (Round your answer to one decimal place.)(b) How long before the profit found in part (a) is predicted to double? (Round your answer to the nearest whole number.) years after 1990

Answer 1

Answer: a) 138.32 and b) 35 years approx.

Explanation:

Since we have given that

`R(t)=21.4e^(0.13t)\\\\C(t)=18.6e^(0.13t)`

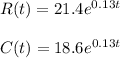
So, Profit is given by

`Profit=R(t)-C(t)\\\\Profit=21.4e^(0.13t)-18.6e^(0.13t)\\\\Profit=e^(0.13t)(21.4-18.6)\\\\Profit=2.8e^(0.13t)`

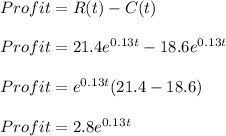
Difference in years of 1990 and 2020=30

So, Profit becomes :

`P(30)=2.8e^(0.13* 30)\\\\P(30)=2.8* 49.40\\\\P(30)=138.32`

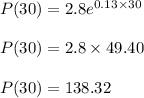
(b) How long before the profit found in part (a) is predicted to double? (Round your answer to the nearest whole number.) years after 1990.

So, profit doubles , we get :

`138.32* 2=2.8e^(0.13t)\\\\276.65=2.8e^(0.13t)\\\\(276.65)/(2.8)=e^(0.13t)\\\\98.80=e^[0.13t}\\\\\ln 98.80=0.13t\\\\4.593=0.13t\\\\(4..593)/(0.13)=t\\\\35.33=t`

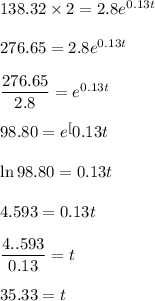
Hence, a) 138.32 and b) 35 years approx.