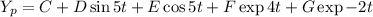Question

Use the annihilator method to determine the form of a particular solution for the given equation. u double prime minus 2 u prime minus 8 equals cosine (5 x )plus 7 Find a differential operator that will annihilate the nonhomogeneity cosine (5 x )plus 7

Answer 1

the particular solution is

Y_{p}= C +D\sin 5t +E\cos 5t + F\exp 4t + G\exp -2t

the differential operator that annihilate the non homogeneous differential equation is

D(D^2+5)

Explanation:

hello,

i believe the non homogeneous differential equation is

`U^('') - 2U^(') - 8= \cos 5x + 7`

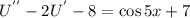
the homogeneous differential equation of the above is

`u^('') -2u^(') -8 =0`

the differential form of the above equation is

`D^2-2D-8=0`

`(D-4)(D+2)=0`

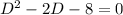
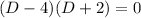
thus the roots are 4 and -2.

thus the solution of the homogenous differential equation is given as

`Y_(h) (t)= Aexp(4t) + Bexp(-2t)`

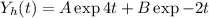
the differential operator of the non homogeneous equation is given as

`(D-4)(D+2)(u)=\cos 5x +7`

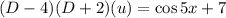
the differential operator
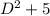`D^2 +5` annihilates
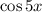`\cos 5x` and the differential operator D annihilates 7

applying
`D(D^2+5)` to both sides of the differential equation we have;

(D-4)(D+2)(u)=\cos 5x +7

`D(D^2+5)(D-4)(D+2)=D(D^2+5)(\cos5x+7)`
`D(D^2+5)(D-4)(D+2)=0`

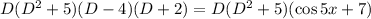
the roots of the characteristic polynomial of the diffrential equation above are
`0, \cmplx 5i, -\cmplx 5i, 4, -2`

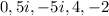
thus the particular solution is

`Y_(p)= Cexp(0)+D\sin 5t +E\cos 5t + F\exp {4t} + G\exp {-2t}`

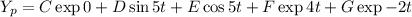
this gives us the particular solution

`Y_(p)= C +D\sin 5t +E\cos 5t + F\exp 4t + G\exp -2t`