Question

The stopping distance of a car is modeled by the function d = 0.05r(r + 2) where d is the stopping distance of the car measured in feet and r is the speed of the car in miles per hour. If skid marks left on the road are 75 feet long, how fast was the car traveling?

Answer 1

The car was moving approximately at a speed of 37.74 miles per hour.

Explanation:

We are given the following in the question:

The stopping distance of a car is given by

`d = 0.05r(r + 2)`

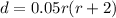
where d is the stopping distance in feet and r is speed of the car in miles per hour.

The stopping distance is 75 feet, we have to find the speed of the car,

Putting d = 75 in the equation, we get,

`75 = 0.05r(r + 2)\\r^2 + 2r = 1500\\r^2 + 2r-1500 = 0\\\\r =(-2\pm √(4-(4)(1)(-1500)))/(2)\\\\r\approx -39.74,37.74`

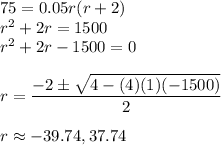
Thus, the car was moving approximately at a speed of 37.74 miles per hour.