Question

The following data contains​ coaches' salaries and team revenues​ (in millions of​ dollars) for ten college basketball teams. Use these data to complete parts​ (a) through​(c).

Salary 0.4 0.8 1.4 1.3 1.2 1.9 0.5 0.9 1.5 0.6

Revenue 4.9 7.5 17.2 18.2 11.5 13.6 8.0 6.0 18.0 8.2

a. Compute the covariance.

b. Compute the coefficient of correlation.

c. What conclusions can you reach about the relationship between a​ coach's salary and​ revenue?

A.There is a strong positive relationship between a​ coach's salary and revenue. As a​ coach's salary​ increases, revenue always increases.

B.There is a moderate positive relationship between a​ coach's salary and revenue. As a​ coach's salary​ increases, revenue tends to increase.

C. There is a slight relationship between a​ coach's salary and revenue. Increases in a​ coach's salary cause increases in revenue.

D.There is no relationship between a​ coach's salary and revenue.

Answer 1

(a) The covariance is 179.05.

(b) The coefficient of correlation between the coach's salary and revenue is 0.7947.

(c) The correct option is (A).

Explanation:

The correlation coefficient is a statistical degree that computes the strength of the linear relationship amid the relative movements of the two variables (i.e. dependent and independent).It ranges from -1 to +1.

The formula to compute correlation between two variables X and Y is:

`r(X,Y)=(Cov(X, Y))/(√(V(X).V(Y)))`

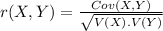
The formula to compute covariance is:

`Cov(X, Y)=n\cdot\sum{XY} - \sum{X}\cdot\sum{Y}`

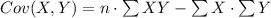
The formula to compute the variances are:

`V(X)=n \sum{X^2}-\left(\sum{X}\right)^2\right\\V(Y)=n \sum{Y^2}-\left(\sum{Y}\right)^2\right`

Let, X = Salary and Y = Revenue.

(a)

Consider the table attached below.

Compute the covariance as follows:

`Cov(X, Y)=n\cdot\sum{XY} - \sum{X}\cdot\sum{Y}`

`=(10* 136.66)-(10.5* 113.1)\\=1366.6-1187.55\\=179.05`

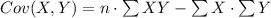
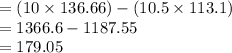
Thus, the covariance is 179.05.

(b)

Compute the variance of X and Y as follows:

`V(X)=n \sum{X^2}-\left(\sum{X}\right)^2\right`

`=(10* 13.17)-(10.5)^(2)\\=21.45`

`V(Y)=n \sum{Y^2}-\left(\sum{Y}\right)^2\right`

`=(10* 1515.79)-(113.1)^(2)\\=2366.29`

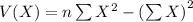
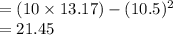
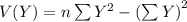
Compute the correlation coefficient as follows:

`r(X,Y)=(Cov(X, Y))/(√(V(X).V(Y)))`

`=(179.05)/(√(21.45* 2366.29))`

`=0.7947`

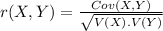
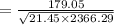
Thus, the coefficient of correlation between the coach's salary and revenue is 0.7947.

(c)

Positive correlation is an association amid two variables in which both variables change in the same direction.

A positive correlation occurs when one variable declines as the other variable declines, or one variable escalates while the other escalates.

A correlation coefficient value between 0.70 to 1.00 is considered as a strong positive relation between the two variables.

The correlation between the coach's salary and revenue is 0.7947. This is implies that there was a strong positive relationship between a​ coach's salary and revenue, i.e. an increase in the salary would have resulted as an increase in the revenue.

Thus, the correct option is (A).