Question

A sample of an ideal gas is in a tank of constant volume. The sample absorbs heat energy so that its temperature changes from 335 K to 1340 K. If v1 is the average speed of the gas molecules before the absorption of heat and v2 their average speed after the absorption of heat, what is the ratio v2

Answer 1

The ratio of v₂/v₁ is 2

Step-by-step explanation:

Here we have Charles law which can be presented as

P₁/T₁ = P₂/T₂

Therefore,

P₂ = T₂ × P₁/T₁

Also from the kinetic theory of gases we have;

`v_(rms) = \sqrt{(3* R* T)/(MW) }`

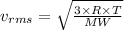
Where:

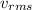`v_(rms)` = Rms speed

R = Universal gas constant

T = Temperature in Kelvin

MW = Molecular weight

We therefore have for the before and after speeds as

`v_1 = \sqrt{(3* R* T_1)/(MW) }` and
`v_2 = \sqrt{(3* R* T_2)/(MW) }`

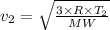
Therefore,

`(v_2)/(v_1 ) = \frac{\sqrt{(3* R* T_2)/(MW) }}{\sqrt{(3* R* T_1)/(MW) }} = \sqrt{((3* R* T_2)/(MW))/((3* R* T_1)/(MW)) } = \sqrt{(T_2)/(T_1) }`

`(v_2)/(v_1 ) = \sqrt{(T_2)/(T_1) } = \sqrt{(1340)/(335) } =\sqrt{(4)/(1) } = 2`

∴ v₂/v₁ = 2.

Answer 2

`(v_(2))/(v_(1))=2`.

Step-by-step explanation:

The average kinetic energy per molecule of a ideal gas is given by:

`\bar{K}=(3k_(B)T)/(2)`

Now, we know that
`\bar{K} = (1/2)m\bar{v}^(2)`

Before the absorption we have:

`(1/2)m\bar{v_(1)}^(2)=(3k_(B)T_(1))/(2)` (1)

After the absorption,

`(1/2)m\bar{v_(2)}^(2)=(3k_(B)T_(2))/(2)` (2)

If we want the ratio of v2/v1, let's divide the equation (2) by the equation (1)

`(v_(2)^(2))/(v_(1)^(2))=(T_(2))/(T_(1))`

`(v_(2))/(v_(1))=\sqrt{(T_(2))/(T_(1))}`

`(v_(2))/(v_(1))=\sqrt{(1340)/(335)}`

`(v_(2))/(v_(1))=√(4)`

Therefore the ratio will be
`(v_(2))/(v_(1))=2`

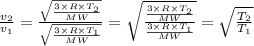
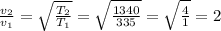
I hope it helps you!