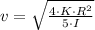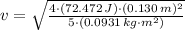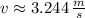1 Answer

Ask a Question

KoPytok · Answer 1 · 2021-12-17T08:16:57+0000

Answer:

a)
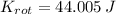$K_(rot) = 44.005\,J$ , b)
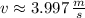$v \approx 3.997\,(m)/(s)$ , c)
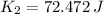$K_(2) = 72.472\,J$ , d)
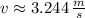
$v \approx 3.244\,(m)/(s)$

Step-by-step explanation:

b) The kinetic energy for a rigid body is the sum of translational and rotational kinetic energy:

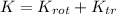
K = K_(rot) + K_(tr)

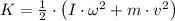
$K = (1)/(2)\cdot \left(I\cdot \omega^(2) + m\cdot v^(2)\right)$

$K = (1)/(2)\cdot \left[I\cdot \left((v)/(R) \right)^(2) +m\cdot v^(2)\right]$

$K = (1)/(2)\cdot \left[(I)/(R^(2))+(3\cdot I)/(2\cdot R^(2)) \right] \cdot v^(2)$

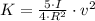
$K = (5\cdot I)/(4\cdot R^(2))\cdot v^(2)$

The speed of the center of mass of the sphere at the initial position is:

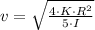
$v = \sqrt{(4\cdot K\cdot R^(2))/(5\cdot I) }$

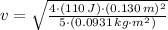
$v = \sqrt{(4\cdot (110\,J)\cdot (0.130\,m)^(2))/(5\cdot \left(0.0931\,kg\cdot m^(2) \right)) }$

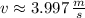
$v \approx 3.997\,(m)/(s)$

a) The kinetic energy associated with the rotation is:

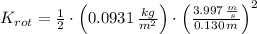
$K_(rot) = (1)/(2)\cdot \left(0.0931\,(kg)/(m^(2))\right)\cdot \left((3.997\,(m)/(s) )/(0.130\,m) \right)^(2)$

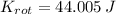
$K_(rot) = 44.005\,J$

It is 40 % of the total initial kinetic energy.

c) The total final kinetic energy is:

$K_(2) = 110\,J - \left[(3\cdot \left(0.0931\,kg\cdot m^(2)\right))/(2\cdot (0.130\,m)^(2)) \right]\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (1.20\,m)\cdot \sin 22.7^(\textdegree)$

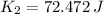
$K_(2) = 72.472\,J$

d) The speed of its center of mass is:

$v = \sqrt{(4\cdot K\cdot R^(2))/(5\cdot I) }$

$v = \sqrt{(4\cdot (72.472\,J)\cdot (0.130\,m)^(2))/(5\cdot \left(0.0931\,kg\cdot m^(2) \right)) }$

$v \approx 3.244\,(m)/(s)$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions