Answer:
The margin of error (M.E) = 3.51
Explanation:
Explanation:-
Given data a large school district in Connecticut wants to estimate the average SAT score of this year’s graduating class.
The district takes a simple random sample of 100 seniors.
The sample size 'n' = 100
given data the sample mean is 510 and the population standard deviation for SAT scores is known to be 75.
mean of the sample = 510
population standard deviation σ = 75.
Given data they want an interval that "likely" contains the true mean, where "likely" means "the procedure has a 68% success rate".
level of significance = 68% =0.68
Z-score of 68% of level of significance = 0.468
Margin of error:-
The margin of error of at 68% of confidence intervals.
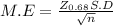

Margin of error = 3.51
Conclusion:-
Margin of error = 3.51 at 68% of confidence interval