Hi there!
We can begin by using Coulomb's Law:
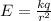
k = Coulomb's Constant (8.99 × 10⁹ Nm²/C²)
E = Electric field strength (N/C)
r = distance from point (m)
q = charge (C)
Since this is a continuous charge, we must use calculus.
We can express this as the following:
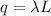
λ = Linear charge density (C/m)
L = Length of rod (m)
Now, since this is an arc, L = s (arc length). Additionally, we must find the differential elements of each:
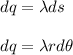
Our new equation is:
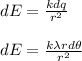
However, we will only take the cosine component of the electric field since the vertical components will cancel out. (Electric fields are a vector). Therefore:
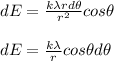
Integrate. For a semicircle, the bounds will be from -π/2 to π/2.
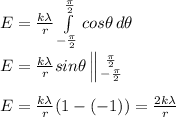
We need to solve for λ, which is Q/ L:
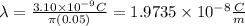
Now, plug and solve for the electric field strength:
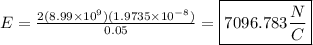
**A diagram was not provided, but if the hemisphere's focus was to the right, the electric field would be to the right, and etcetera.