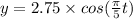Question

At a given time it is noted that the buoy moves a total of 5.5 feet from its low point to its high point, and that it returns to its high point every 8 seconds. Write an equation that describes the motion of the buoy if it is at its high point at time t

Answer 1

The equation is
`y=2.75* cos((\pi )/(5) t)`

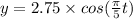
Explanation:

Considering the buoy as a solid ball performing the simple harmonic motion. At any time t, the angular velocity of the ball be ω and the maximum displacement for the ball is A also its amplitude.

So,

The equation for the displacement can be given as y = A c o s (ω t) .

Lets find the amplitude as the question says that the buoy moves from its low point to its high point meaning that the amplitude is half of it as we consider it from origin.

⇒ Amplitude,
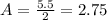`A =(5.5)/(2) = 2.75` ft

⇒ Angular velocity,
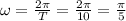`\omega = (2\pi )/(T) = (2\pi )/(10) =(\pi )/(5)` ...as time period (T) = 10 sec

To find the equation we have to arrange them in
`y=A* cos(\omega t)` .

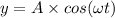Plugging the values in the above equation.

⇒
`y=A* cos(\omega t)`

⇒
`y=2.75* cos((\pi )/(5) t)`

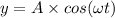
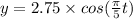
Equation that describes the motion of the buoy if it is at its high point at time t is
`y=2.75* cos((\pi )/(5) t)`