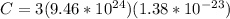Question

For most solids at room temperature, the specific heat is determined by oscillations of the atom cores in the lattice (each oscillating lattice site contributes 3kT of energy, by equipartition), as well as a contribution from the mobile electrons (if it's a metal). At room temperature the latter contribution is typically much smaller than the former, so we will ignore it here. In other words, you can reasonably estimate the specific heat simply by counting the number of atoms! Use this fact to estimate the specific heat of copper (atomic mass = 63.6), given that the specific heat of aluminum (atomic mass = 27.0) is 900 J/kg-K.

Answer 1

The specific heat of copper is
`C= 392 J/kg\cdot ^o K`

Step-by-step explanation:

From the question we are told that

The amount of energy contributed by each oscillating lattice site is
`E =3 kT`

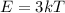
The atomic mass of copper is
`M = 63.6 g/mol`

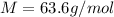
The atomic mass of aluminum is
`m_a = 27.0g/mol`

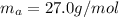
The specific heat of aluminum is
`c_a = 900 J/kg-K`

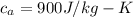
The objective of this solution is to obtain the specific heat of copper

Now specific heat can be defined as the heat required to raise the temperature of 1 kg of a substance by
`1 ^o K`

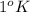
The general equation for specific heat is

`C = (dU)/(dT)`

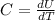
Where
`dT` is the change in temperature

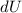`dU` is the change in internal energy

The internal energy is mathematically evaluated as

`U = 3nk_BT`

Where
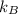`k_B` is the Boltzmann constant with a value of
`1.38*10^(-23) kg \cdot m^2 /s^2 \cdot ^o K`

T is the room temperature

n is the number of atoms in a substance

Generally number of atoms in mass of an element can be obtained using the mathematical operation

`n = (m)/(M) * N_A`

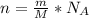
Where
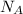`N_A` is the Avogadro's number with a constant value of
`6.022*10^(23) / mol`

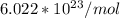
M is the atomic mass of the element

m actual mass of the element

So the number of atoms in 1 kg of copper is evaluated as

`m = 1 kg = 1 kg * (10000 g)/(1kg ) = 1000g`

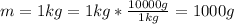
The number of atom is

`n = (1000)/(63.6) * (6.0*0^(23))`

`= 9.46*10^(24) \ atoms`

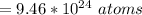
Now substituting the equation for internal energy into the equation for specific heat

`C = (d)/(dT) (3 n k_B T)`

`=3nk_B`

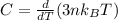
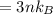
Substituting values

`C = 3 (9.46*10^(24) )(1.38 *10^(-23))`

`C= 392 J/kg\cdot ^o K`