Question

The number of pupils in school A is equal to half the number of pupils in school B. The ratio of the boys in school A and the boys in school B is 1:3 and the ratio of the girls in school A and the girls in school B is 3:5. The number of boys in school B is 200 higher than the number of boys in school A. Find the number of boys and girls in each school.

Answer 1

Answer: 100 boys, 300 girls in School A. 300 boys,500 girls in School B

Explanation:

Answer 2

There are 100 boys and 300 girls in School A and there are 300 boys and 500 girls in School B .

Explanation:

The ratio of the boys in school A and the boys in school B is 1:3

Let the ratio be x

No. of boys in School A = x

No. of boys in School B = 3x

We are given that The number of boys in school B is 200 higher than the number of boys in school A.

So,
`x+200=3x`

`200=3x-x`

`200=2x`

`(200)/(2)=x`

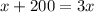
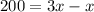
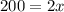
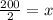
100=x

So, No. of boys in School A = x = 100

No. of boys in School B = 3x =3(100)=300

We are given that the ratio of the girls in school A and the girls in school B is 3:5.

Let the ratio be y

So, No. of girls in School A = 3y

No. of girls in School B = 5y

So, Total No. of students in School A= No. of boys in school A + No. of girls in school A=100+3y

Total No. of students in School B= No. of boys in school B + No. of girls in school B=300+5y

We are given that The number of pupils in school A is equal to half the number of pupils in school B.

So,
`100+3y=(1)/(2)(300+5y)`

`200+6y=300+5y`

`y=100`

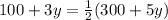
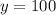
No. of girls in School A = 3y=3(100)=300

No. of girls in School B = 5y=5(100)=500

Hence there are 100 boys and 300 girls in School A and there are 300 boys and 500 girls in School B .