Answer:
The correct option is 16.041 ounces.
Explanation:
A single mean test can be used to determine whether the average amount of shampoo per bottle is 16 ounces.
The hypothesis can be defined as:
H₀: The average amount of shampoo per bottle is 16 ounces, i.e. μ = 16.
Hₐ: The average amount of shampoo per bottle is different from 16 ounces, i.e. μ ≠ 16.
The information provided is:

We can compute a 90% confidence interval to determine whether the population mean is 16 ounces or not.
Since the population standard deviation is known we will compute the z-interval.
The critical value of z for 90% confidence interval is:
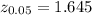
*Use a z-table.
Compute the 90% confidence interval for population mean as follows:
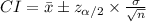
Since the sample size is quite large, according to the law of large numbers the on increasing the sample size, the mean of the sample approaches the whole population mean.
So, the 90% confidence interval estimate for sample mean is:
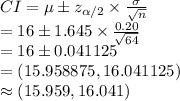
Thus, the correct option is 16.041 ounces.