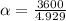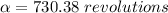Answer:
The gravity at planet X is

The value of
 on the moon is
on the moon is
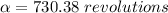
Step-by-step explanation:
From the question we are told that
The clocks hour hand makes
 revolution every 1 hour which is 3600 sec
revolution every 1 hour which is 3600 sec
this implies that the time peroid for 1 revolution would be
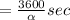
The peroid for a pendulum is mathematically represented as

Where L is the pendulum length
g is the acceleration due to gravity
Let assume that we have a pendulum that counts in second on earth
This implies that its peroid would be = 2 second
i.e one second to swimg forward and one second to swing back to its original position
Now the length of this pendulum on earth is
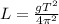 [Making L the subject in above equation]
[Making L the subject in above equation]
Substituting values

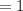
When the same pendulum is taken to planet X the peroid would be
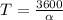
Recall this value was obtained above for 1 revolution (from start point to end point back to start point)
So the acceleration due to gravity on this planet would be mathematically represented as
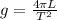 [making g the subject in the above equation]
[making g the subject in the above equation]
substituting values
![g = (4 * 3.142^2 * 1)/([ (3600)/(\alpha ) ]^2)](https://img.qammunity.org/2021/formulas/physics/college/qlo00brmft62pxq8zw35zi2ikpnnd7yp0v.png)

On moon the acceleration due to gravity has a constant value of

The period of this pendulum on the moon can be mathematically evaluated as
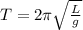
substituting value
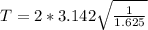
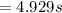
given that
 {Note 1 revolution takes a peroid }
{Note 1 revolution takes a peroid }
Making
 the subject of the formula
the subject of the formula