Answer:
The value of r to have maximum profit is 3/25 ft
Explanation:
To find:
The size of the sphere so that the profit can be maximized.
Manufacturing cost of the solid sphere = $500/ ft^3
Selling price of sphere (on surface area) = $30 / ft^2
We see that the manufacturing cost dealt with he volume of the sphere where as the selling price dealt with the surface area.
So,
To maximize the profit (P) .
We can say that:
⇒
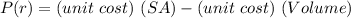
⇒
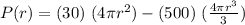
⇒
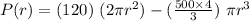
⇒
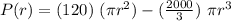
Differentiate "
 " and find the "
" and find the "
 " value then double differentiate "
" value then double differentiate "
 ", plug the "
", plug the "
 " values from
" values from
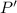 to find the minimum and maximum values.
to find the minimum and maximum values.
⇒

⇒
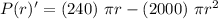
Finding r values :
⇒
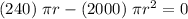
Dividing both sides with 240π .
⇒
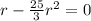 ⇒
⇒
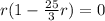
⇒
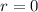 and
and

To find maxima value the double differentiation is :
⇒
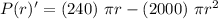 ...first derivative
...first derivative
Double differentiating :
⇒
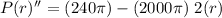 ...second derivative
...second derivative
⇒

Test the value r = 3/25 dividing both sides with 240π
⇒
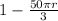
⇒

⇒
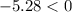
It passed the double differentiation test.
Extra work :
Thus:
⇒
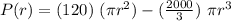
⇒
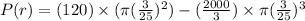
⇒
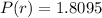
Finally r =3/25 ft that will maximize the profit of the manufacturing company.