Answer:
Length of pipe to Chesterville is 8.376 miles and
Length of pipe to Denton is 5.46 miles
Explanation:
Here we have
The distance of Chesterville from the river is 3 miles, while the distance of Denton from the river is 5 miles
The bank of the river is 10 miles long
Therefore, we have
If x is the distance from the point directly opposite to Chesterville to the location of the water works, the equation is;
Cost to Chesterville =
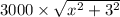
Cost to Denton =
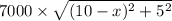
Total cost is then;
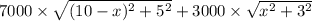
We differentiate the above equation and equate it to zero to get the minimum cost as
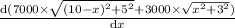 = 0
= 0
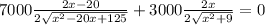
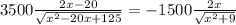
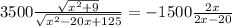

Solving the quartic equation we get
x = 7.82 miles
Therefore the length of is given as
Length of pipe to Chesterville
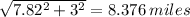
Length of pipe to Denton =
 .
.